La loi normale

twitch
Rnewbies
analyse de données
statistiques
Author

Marie Vaugoyeau

Published

22 November 2022

Note

Twitch du 22 novembre 2022 La vidéo n’est malheureusment plus disponible suite à une erreur de manipulation 🫣
Code disponible sur GitHub

library(tidyverse)

# fixe la graine à 105
set.seed(105)

Introduction

Les lois de proababilités

Une loi de probabilité revient à prévoir le comportement d’une expérience aléatoire. Les grandes lois de probabilité sont basées sur le fonctionnement de jeu de hasard et ont été ensuite formalisées.
Naturellement, tout le monde comprend que lorsqu’on joue à lancer une pièce (équilibrée) au hasard, chacune des faces à autant de chance de sortir.
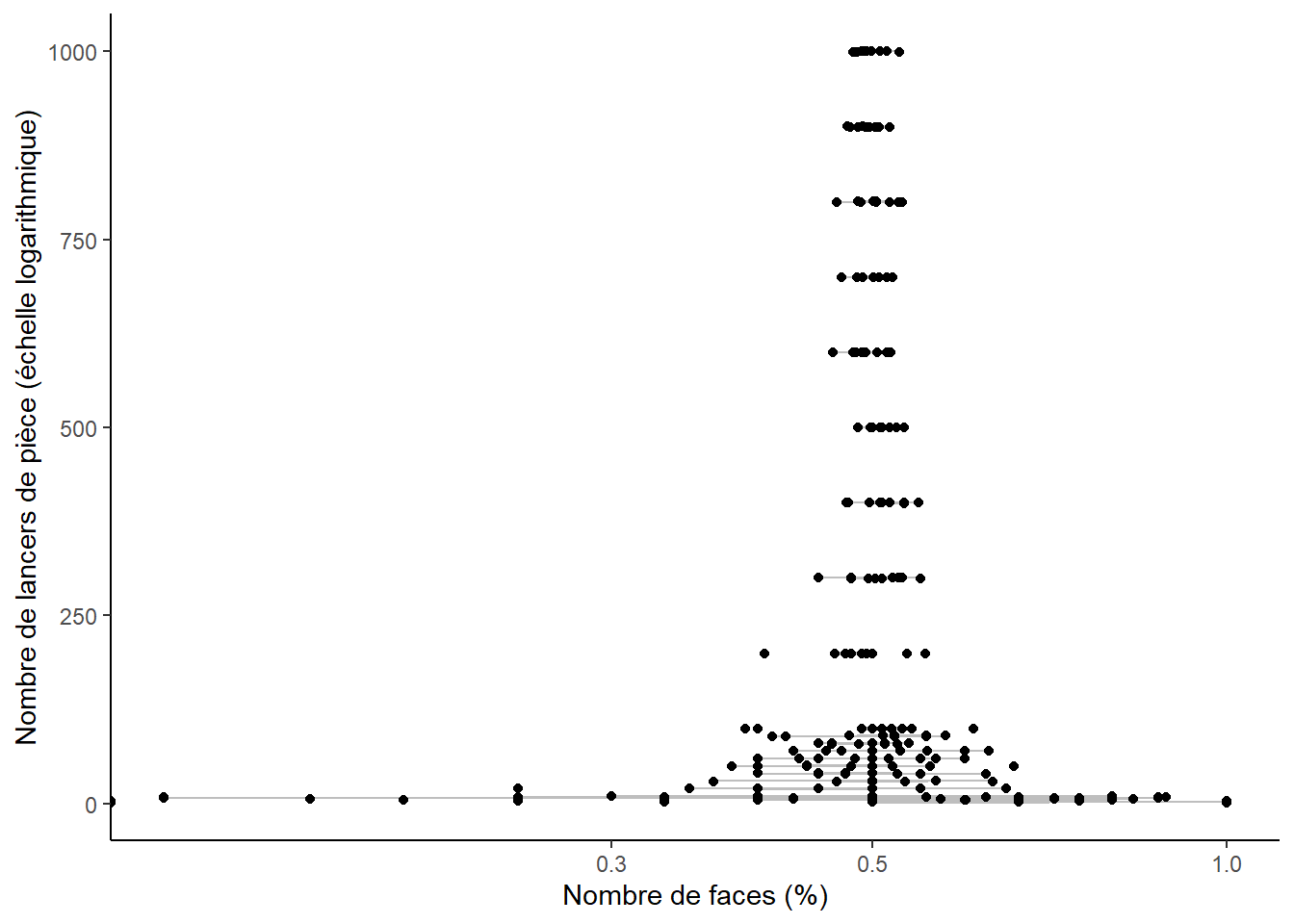
Il est impossible de prévoir le nombre de piles et de faces pour un petit nombre de lancers, par exemple six.
Par contre, plus ce nombre augmente, plus on peut prévoir le nombre de fois que le côté face va sortir, car le nombre de lancers équilibre le résultat.

# création d'un vecteur contenant le nombre de lancers
nb_lancers <- c(
  1:9, # 1, 2, 3... 9
  seq(from = 10, to = 100, by = 10), # 10, 20... 100
  seq(from = 200, to = 1000, by = 100) # 200, 300... 1000
)

# 10 simulations pour chaque valeurs de nb_lancers de pièces
purrr::map(
  c(1:10),
  ~ bind_rows(
    bind_cols(
      nb_lancers = nb_lancers,
      nb_lancers %>% 
        purrr::map(
          ~ rbinom(.x, 1, 0.5)
        ) %>% 
        purrr::map(sum) %>% 
        purrr::map(as_tibble) %>% 
        bind_rows() %>% 
        rename(nb_faces = value)
    )
  )
) %>% 
  bind_rows() %>% # mise en commun des lignes
  mutate(
    pourcentage_face = nb_faces /nb_lancers # calcul du pourcentage de réussites
  ) %>% # création du graphique
  ggplot() + 
  aes(y = nb_lancers, x = pourcentage_face, group = nb_lancers) +
  geom_boxplot(color = "grey") + # ajout des boîtes à moustaches
  geom_jitter() + # ajout des points
  scale_x_log10() + # choix d'une échelle logarthmique
  theme_classic() +
  labs(
    y = "Nombre de lancers de pièce (échelle logarithmique)",
    x = "Nombre de faces (%)"
  )

Origine de la loi normale

Si la loi de probabilité uniforme est la plus intuitive, la loi de probabilité normal est la plus couramment utilisée. En effet, c’est celle qui est la plus proche des phénomènes biologiques.

Note

La loi normale est aussi appelée loi gaussienne, loi de Gauss ou de Laplace-Gauss des noms de Laplace et Gauss, deux scientifiques du XVIIIème siècle qui l’ont étudiée.

Contrairement aux lois binomiales et de Poisson, la loi normale est une loi de probabilité continue définie par deux paramètres : son espérance (µ) et sa variance (σ). Sa densité de probabilité s’écrit comme suit.
Si X ∽ Ν(μ,σ²) alors \[ f(x)=\frac{1}{(σ√2π)}{e^{\frac{-1}{2} ({\frac{x-μ}{σ})^2}}} \] pour tous \[ x ∈ {R^+} \]
C’est une densité de probabilité et non une fonction de masse qui permet de la définir.
La densité de probabilité est symétrique, le centre étant l’espérance, l’écart-type la largeur du pic comme visible sur la figure.

# choix de l'intervalle de représentation
intervalle <- seq(-15, 15, 0.1)

# loi normale de paramètres µ égale à -5, -3, 0 ou 3 et σ égale à 2, 0.8, 1 ou 3
tibble(
  loi_normale = 
    rep(
      c(
        "µ = 0 & \U03B4 = 1", 
        "µ = 3 & \U03B4 = 3", 
        "µ = -3 & \U03B4 = 0.8", 
        "µ = -5 & \U03B4 = 2"
      ), 
      each = length(intervalle)
    ),
  x = rep(intervalle, 4),
  densite = 
    c(
      dnorm(intervalle, mean = 0, sd = 1),
      dnorm(intervalle, mean = 3, sd = 3),
      dnorm(intervalle, mean = -3, sd = 0.8),
      dnorm(intervalle, mean = -5, sd = 2))
) %>% 
  ggplot() +
  aes(x = x, y = densite, color = loi_normale) +
  geom_line(size = 1) +
  theme_classic() +
  scale_color_manual(values = c("blue", "dark red", "black", "gold")) +
  ylab("densite de probabilité (f(x))") +
  labs(color = "Loi normale")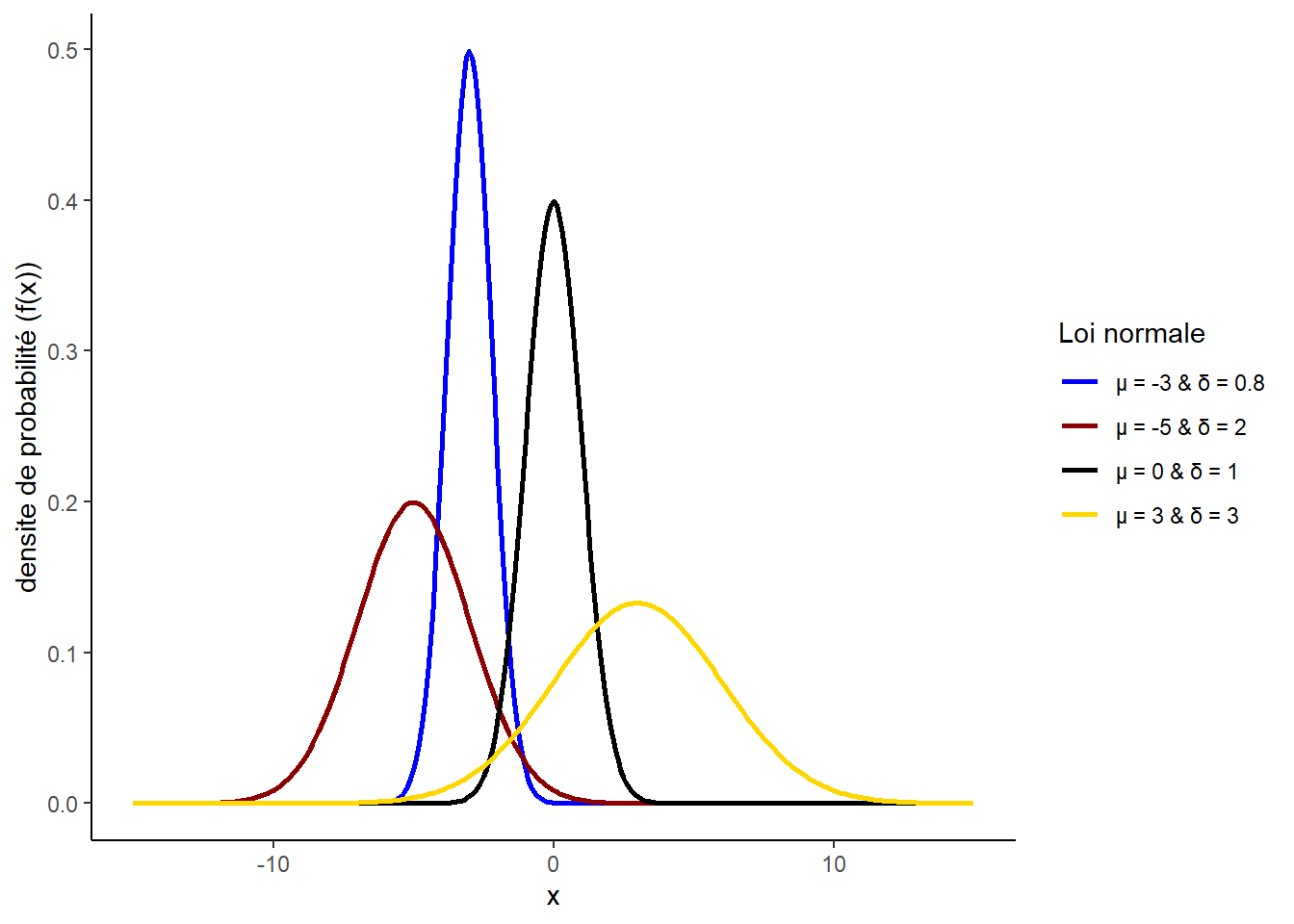

ggsave("img/loi_normale.png")

Approximation

Les évènements aléatoires quel qu’ils soient, rendent impossible la prédiction exacte.
Cela signifie que quand on rejette à 5%, dans 5 cas sur 100, c’est vrai mais on le rejette quand même !

# choix de l'intervalle de représentation
intervalle <- seq(-5, 5, 0.1)

# test bilatéral
bilateral <- tibble(
  x = intervalle,
  "densité" = dnorm(intervalle, mean = 0, sd = 1),
  region = 
    case_when(
      x < qnorm(0.025) ~ "région critique basse",
      x < qnorm(0.975) ~ "région de confiance",
      TRUE ~ "région critique haute"
    )
) %>% 
  ggplot() +
  aes(x = x, y = `densité`) +
  geom_line(size = 1) +
  geom_area(aes(fill = region)) +
  scale_fill_manual(values = c("blue", "red", "green")) +
  geom_vline(xintercept = qnorm(0.025), size = 1, linetype = "dashed") + 
  geom_vline(xintercept = qnorm(0.975), size = 1, linetype = "dashed") + 
  geom_text(aes(x = -4, y = 0.06, label = "2,5 % des valeurs")) +
  geom_text(aes(x = 4, y = 0.06, label = "2,5 % des valeurs")) +
  geom_text(aes(x = 0, y = 0.42, label = "95 % des valeurs")) +
  theme_classic()

# test unilatéral à gauche
unilateral_gauche <- tibble(
  x = intervalle,
  "densité" = dnorm(intervalle, mean = 0, sd = 1),
  region = 
    case_when(
      x < qnorm(0.05) ~ "région critique basse",
      TRUE ~ "région de confiance"
    )
) %>% 
  ggplot() +
  aes(x = x, y = `densité`) +
  geom_line(size = 1) +
  geom_area(aes(fill = region)) +
  scale_fill_manual(values = c("blue", "green")) +
  geom_vline(xintercept = qnorm(0.05), size = 1, linetype = "dashed") + 
  geom_text(aes(x = -3.5, y = 0.06, label = "5 % des valeurs"), size = 2) +
  geom_text(aes(x = 0, y = 0.42, label = "95 % des valeurs"), size = 2) +
  theme_classic() +
  theme(legend.position = "none")

# test unilatéral à droite
unilateral_droit <- tibble(
  x = intervalle,
  "densité" = dnorm(intervalle, mean = 0, sd = 1),
  region = 
    case_when(
      x > qnorm(0.95) ~ "région critique haute",
      TRUE ~ "région de confiance"
    )
) %>% 
  ggplot() +
  
  aes(x = x, y = `densité`) +
  geom_line(size = 1) +
  geom_area(aes(fill = region)) +
  scale_fill_manual(values = c("red", "green")) +
  geom_vline(xintercept = qnorm(0.95), size = 1, linetype = "dashed") + 
  geom_text(aes(x = 3.5, y = 0.06, label = "5 % des valeurs"), size = 2) +
  geom_text(aes(x = 0, y = 0.42, label = "95 % des valeurs"), size = 2) +
  theme_classic() +
  theme(legend.position = "none")

library(cowplot)
ggdraw() +
  draw_plot(bilateral, 0, .5, 1, .5) +
  draw_plot(unilateral_gauche, 0, 0, .5, .5) +
  draw_plot(unilateral_droit, .5, 0, .5, .5)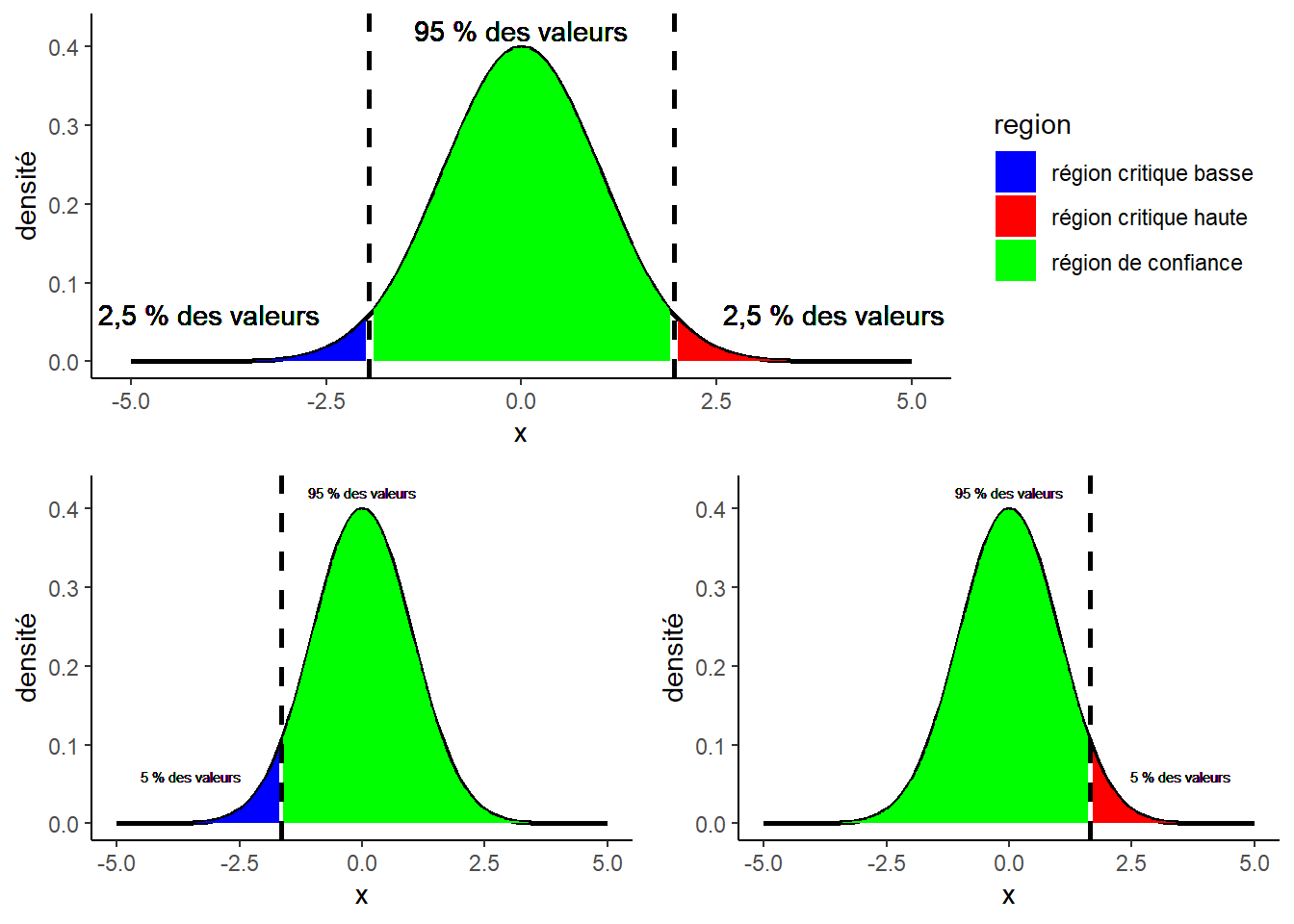

Sur les graphiques les parties rouges et bleues sont vraies mais on les rejette.

Utilité de la loi normale

Un grand nombre de tests est basé sur des données suivant une loi normale : ACP, modèle linéaire, ANOVA…
Si les données ne suivent pas de loi normale il ne faut pas faire ses tests !

Iris : jeu de données utilisé

Iris est un jeu de données avec les longueurs et largeurs de pétales et sépales mesurées sur 150 fleurs d’iris selon trois espèces (50 fleurs par espèce).

iris %>% View()

iris %>% 
  ggplot() +
  aes(x = Petal.Length) +
  geom_histogram()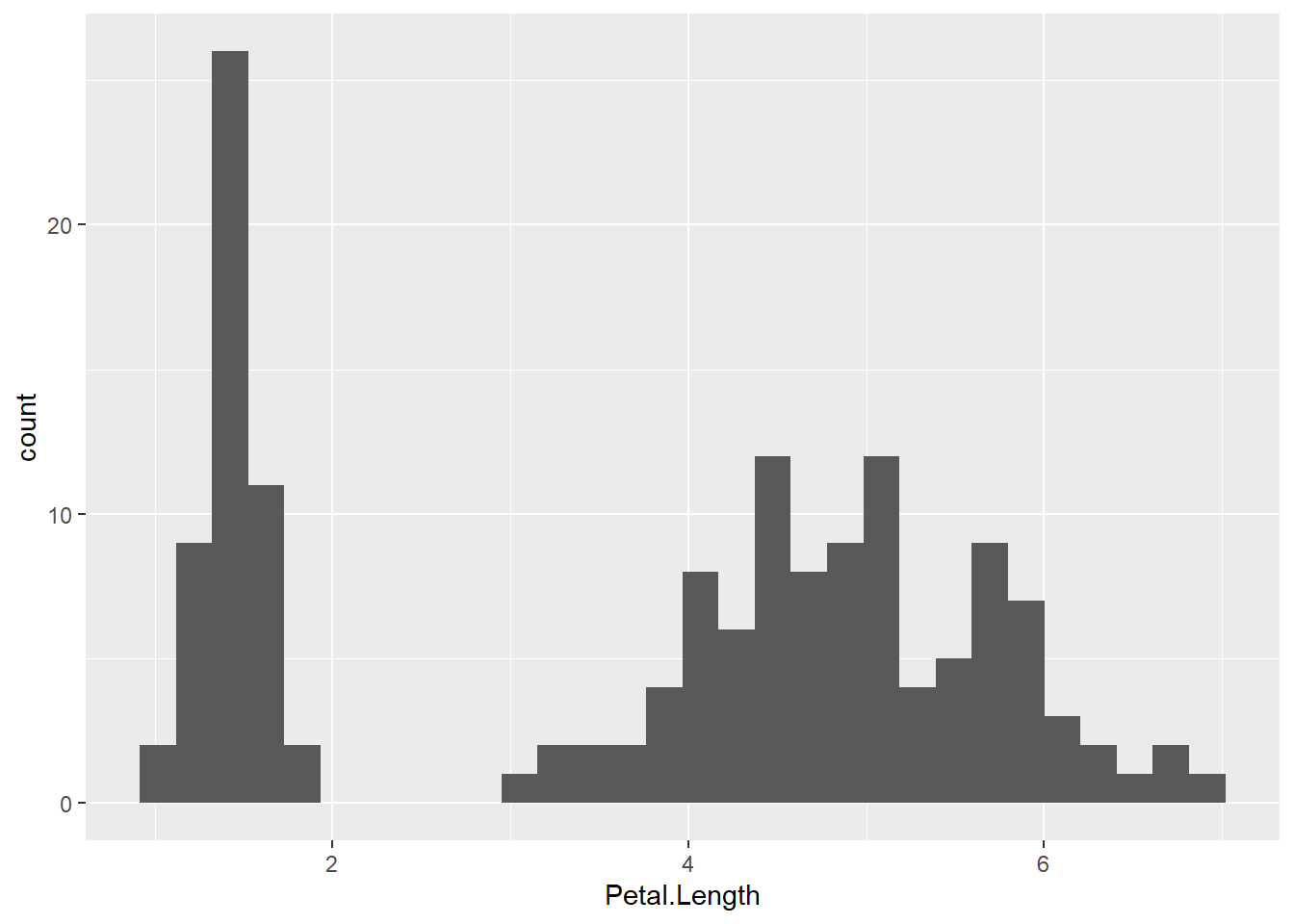

Le test de Shapiro-Wilk

Le test d’hypohtèses

1ère étape : Définir les hypothèses

Hypothèse nulle, H0 : les données suivent une loi normale
Hypothèse alternative, H1 : les données ne suivent pas une loi normale

2ème étape : Formaliser mathématiquement les hypothèses

H0 : X -> N(µ, σ²)
H1 : X –>- N(µ, σ²)

3ème étape : Tester si l’hypothèse nulle est probable ou doit-être rejetée

Si la p-valeur > 0.05, H0 n’est pas rejeté donc les données suivent une loi normale (à vérifier graphiquement)
Sinon les données ne suivent pas une loi normale.

La statistique de test

\[ {\displaystyle W= {\left (\sum \limits _ {i=1}^ {n}a_ {i}x_ { (i)}\right)^ {2} \over \sum \limits _ {i=1}^ {n} (x_ {i}- {\overline {x}})^ {2}}} \]

Réalisation du test

Le test de Shapiro-Wilk ne peut pas être utilisé quand il y a plus de 5000 valeurs.
Il doit être utilisé sur un vecteur et non sur une table entière.

shapiro.test(rnorm(n = 6000, mean = 5, sd = 3))
Error in shapiro.test(rnorm(n = 6000, mean = 5, sd = 3)): la taille de l'échantillon doit être comprise entre 3 et 5000
shapiro.test(
  iris$Petal.Length
)

    Shapiro-Wilk normality test

data:  iris$Petal.Length
W = 0.87627, p-value = 7.412e-10
ggplot(iris) +
  aes(x = Petal.Length, fill = Species) +
  geom_histogram(bins = 35)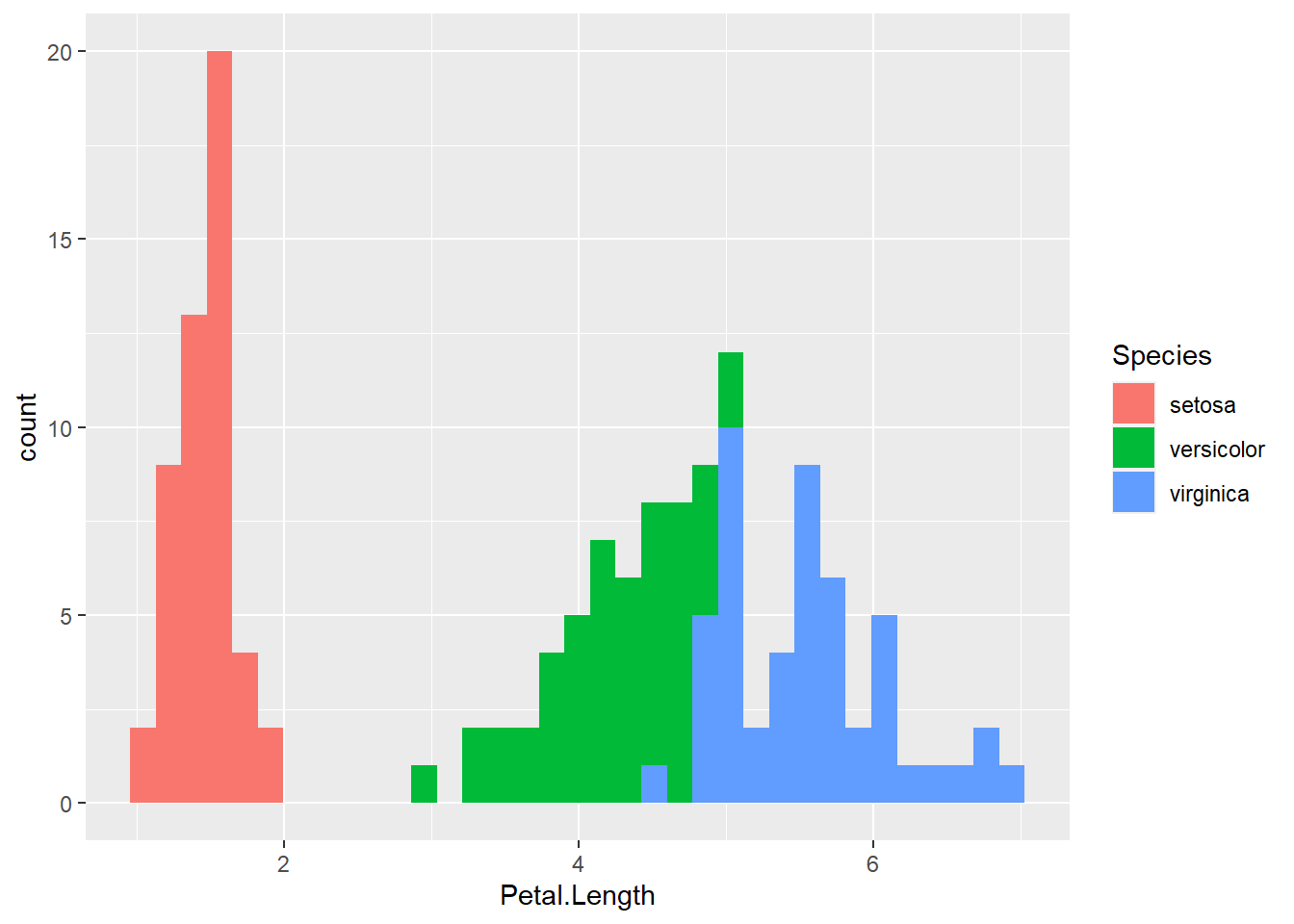

shapiro.test((iris %>% filter(Species == "setosa"))$Petal.Length)

    Shapiro-Wilk normality test

data:  (iris %>% filter(Species == "setosa"))$Petal.Length
W = 0.95498, p-value = 0.05481
shapiro.test((iris %>% filter(Species == "versicolor"))$Petal.Length)

    Shapiro-Wilk normality test

data:  (iris %>% filter(Species == "versicolor"))$Petal.Length
W = 0.966, p-value = 0.1585
iris %>% 
  filter(Species == "setosa") %>% 
  ggplot(aes(x = Petal.Length)) +
  geom_histogram()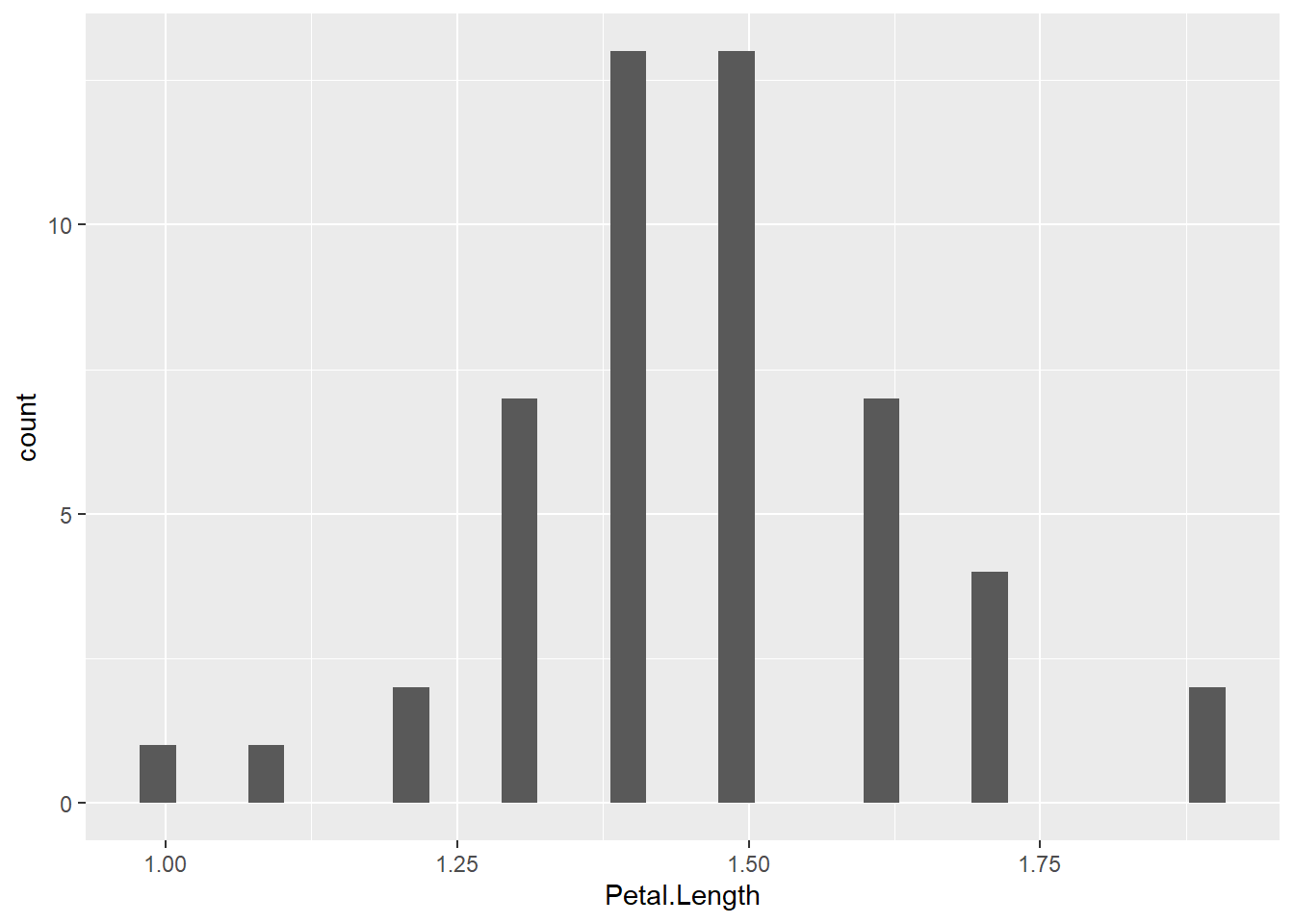

iris %>% 
  filter(Species == "versicolor") %>% 
  ggplot(aes(x = Petal.Length)) +
  geom_histogram()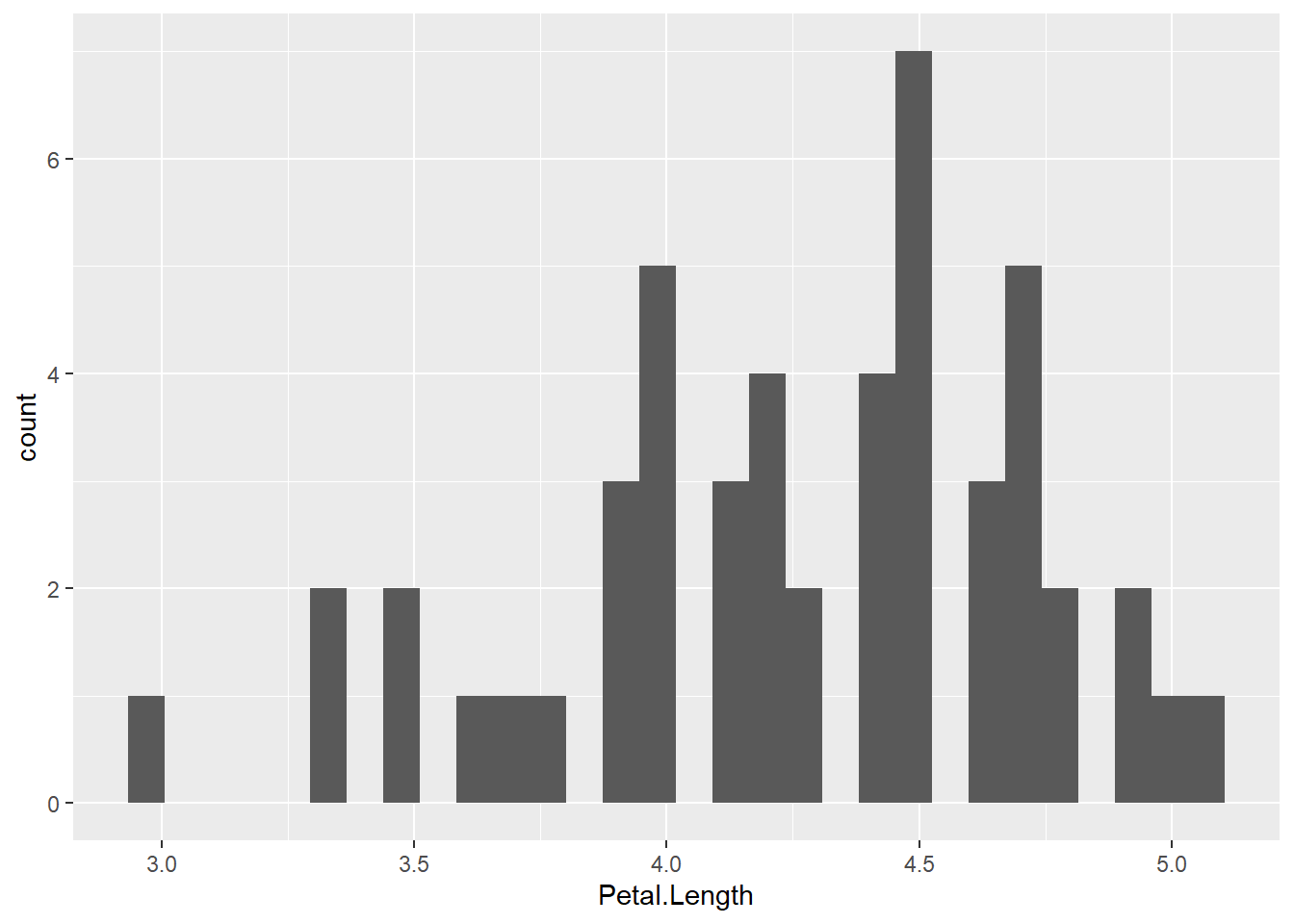

QQplot

Objectif du QQplot

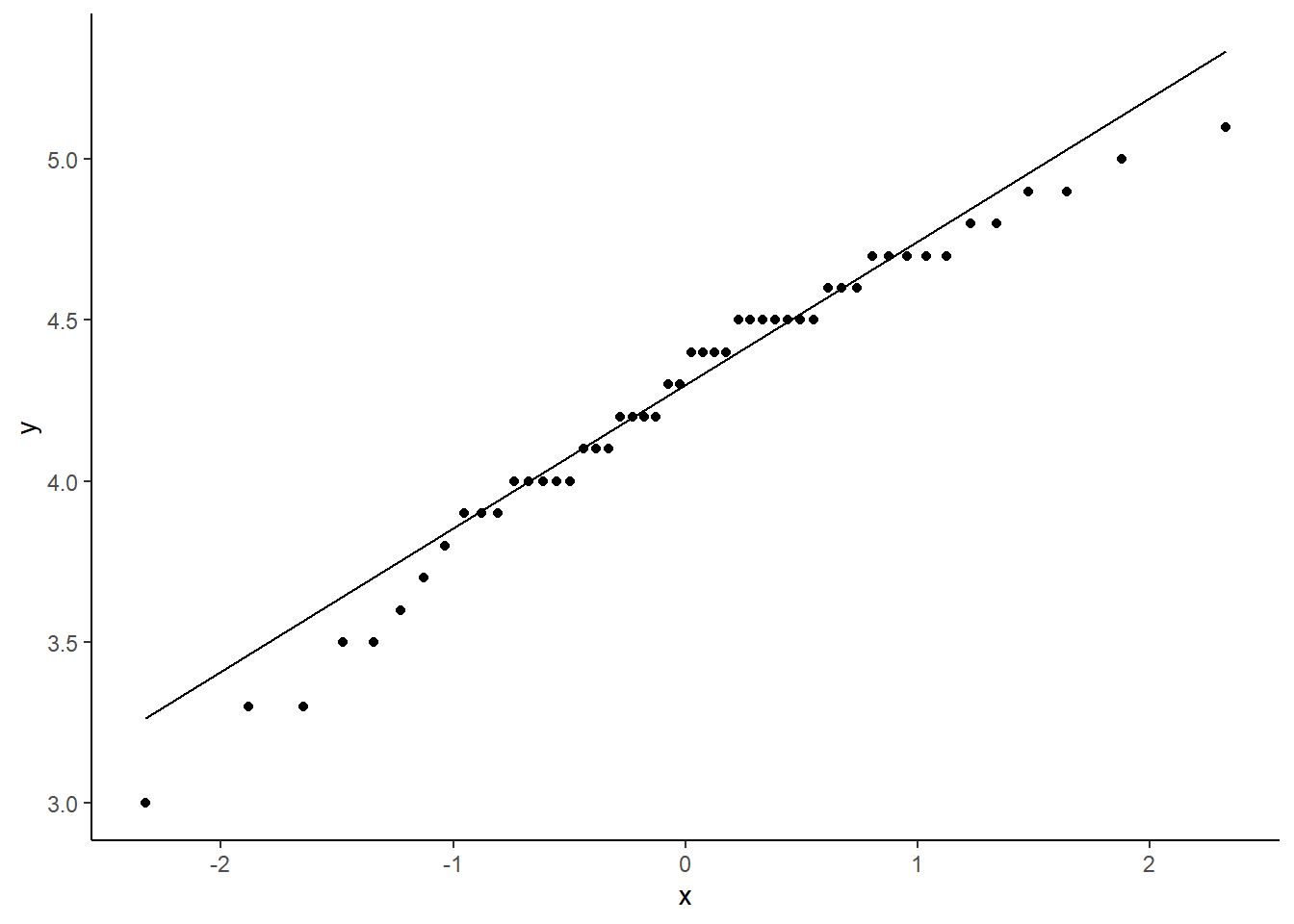
Tester la normalité des données graphiquement en représentant les données réelles et celles attendus selon une loi normale.

Réalisation du graphique

iris %>%
  ggplot() +
  aes(sample = Petal.Length) +
  geom_qq() +
  geom_qq_line(color = "dark red", size = 1) +
  theme_classic()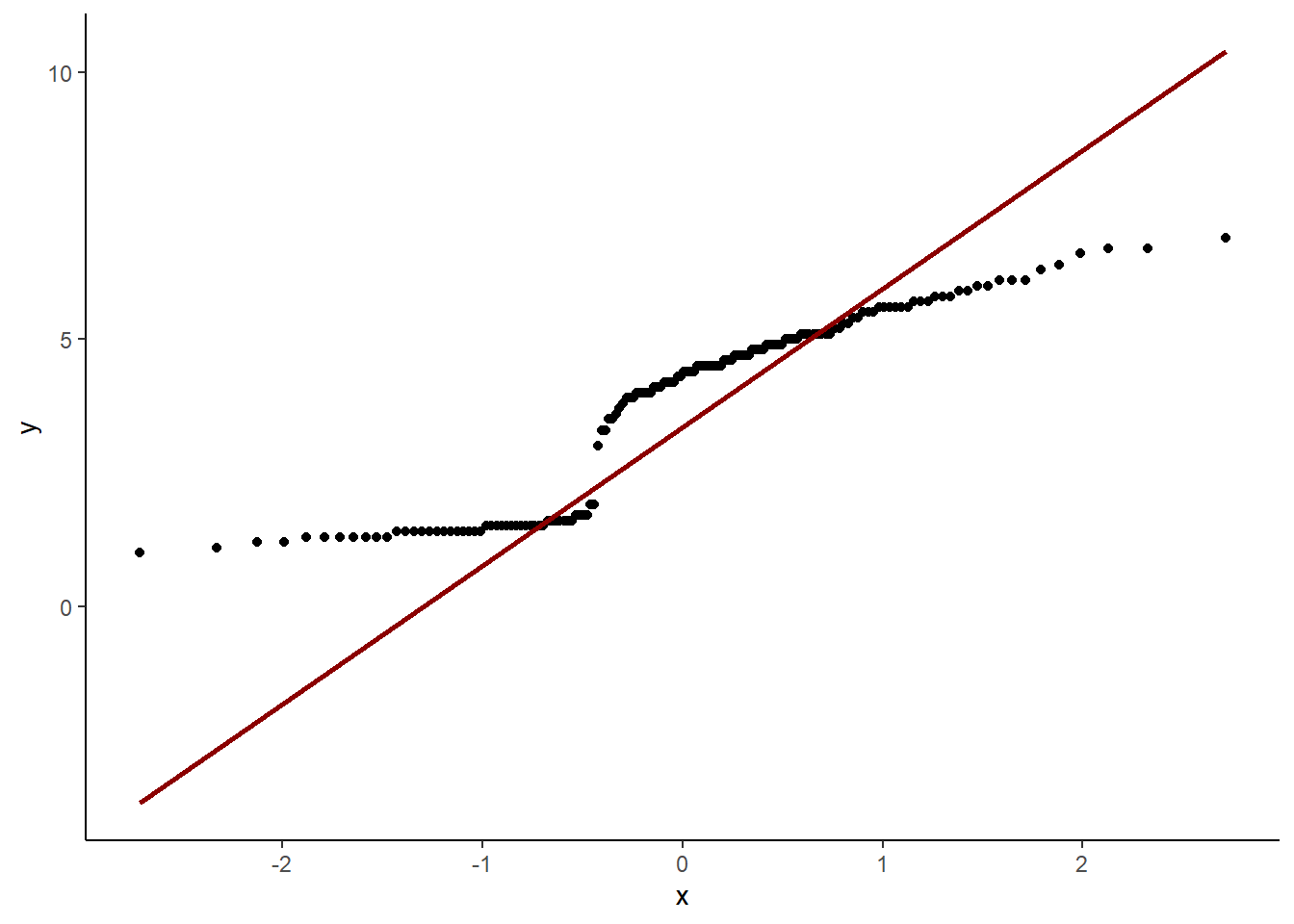

iris %>%
  filter(Species == "setosa") %>% 
  ggplot() +
  aes(sample = Petal.Length) +
  geom_qq() +
  geom_qq_line(color = "dark red", size = 1) +
  theme_classic()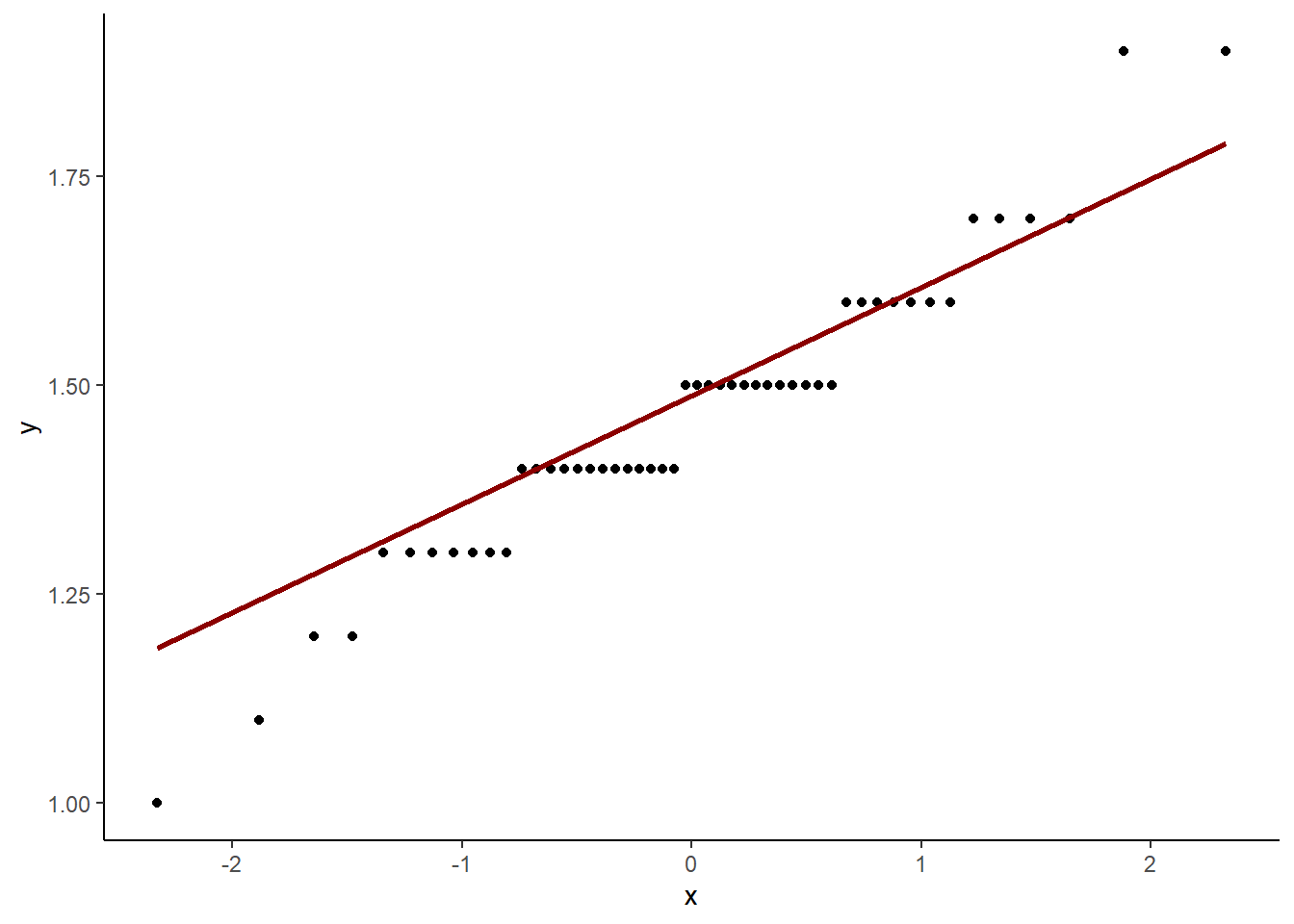

iris %>% 
  filter(Species == "versicolor") %>% 
  ggplot() +
  aes(sample = Petal.Length) +
  geom_qq() +
  geom_qq_line() +
  theme_classic()

Back to top